
Coloring: This strategy involves assigning colors (usually two) to candidates and using the relationships between these colors to make deductions.
It allows for deductions by creating chains of eliminations based on the relationships between the three numbers.
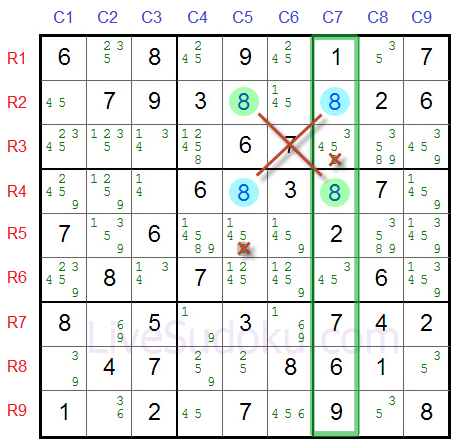
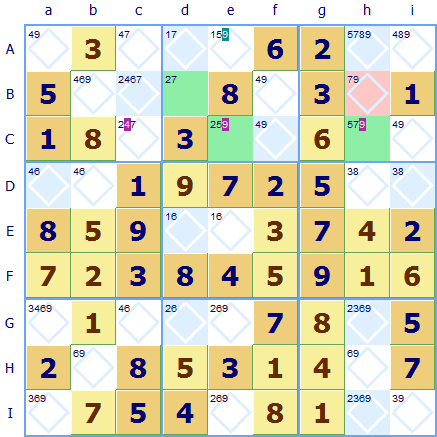
XYZ-Wing: XYZ-Wing involves three cells and three numbers, with each number belonging to a different candidate list. By utilizing a specific pattern of candidate numbers, you can make deductions that lead to solving other squares. Y-Wing: Y-Wing is an advanced strategy that involves three cells and three numbers. It involves finding three rows or three columns where the same number can only occur in the same three positions, allowing for further eliminations. 
Swordfish: Similar to X-Wing, Swordfish expands the concept to three rows or three columns.By eliminating that number as a possibility in the corresponding rows or columns, you can make further deductions. X-Wing: X-Wing involves finding two rows or two columns where the same number can only occur in the same two positions.These numbers can then be eliminated as possibilities from other squares in the unit. Hidden Pairs and Triples: This strategy focuses on identifying two or three candidate numbers that only appear in the same two or three squares within a unit.Naked Pairs and Triples: When two or three squares in a unit (row, column, or box) have the same two or three candidate numbers, those numbers can be eliminated as possibilities from other squares in the unit.Singleton Technique: This strategy involves identifying squares that have only one possible candidate number based on the numbers already present in the row, column, and box.If you get really stuck then we have an online Sudoku Solver to help you solve the most challenging Sudoku puzzles. Remember that mastering XYZ-Wing requires practice and understanding of candidate number relationships.
#Xyz wing sudoku strategy update
Update the puzzle: After making deductions using XYZ-Wing, reassess your puzzle and look for additional opportunities to apply this strategy.īy leveraging this complex technique, you can uncover deductions that may not be apparent through simpler strategies. This will help you eliminate candidates from other squares based on whether or not they have XYZ numbers. Start by considering implications from eliminating candidates in the first and third cells. Create chains of eliminations: Based on the XYZ-Wing pattern, create chains of eliminations that lead to deductions. Consider how their presence or absence in certain cells affects other squares in the puzzle. Examine relationships: Focus on the relationships between the XYZ numbers in the pattern. However, there should be no direct common candidate between the first and third cells. The chain follows a structure where one cell shares a common candidate with the second cell, and the second cell shares a common candidate with the third cell. Identify the XYZ-Wing pattern: Look for a pattern where the three cells form a chain, with each cell having a different candidate number (XYZ). Analyze the puzzle: Examine the grid and identify three cells that have candidate numbers. It is used to identify patterns of three cells and three candidate numbers that lead to deductions and solve other squares in the puzzle. The XYZ-Wing strategy is indeed an advanced solving technique in Sudoku puzzles. ← Sudoku Strategies Sudoku: XYZ-Wing Strategy and Techniques







 0 kommentar(er)
0 kommentar(er)
